I have a symbolism problem. The problem is, essentially, that the symbols that have a strong resonance for me have meaning derived from a toxic culture. The meanings they have for me that seem so deep and magic(k)al are inextricably linked to cultural appropriation, sexism, racism, ableism, homophobia and all the other memetic toxins of modern WEIRD culture.
It’s a problem because even if I could come up with a new symbol that is utterly without historical contextual problems, it would lack two things; first, the communication of an idea, and second, the conceptual relevance for me internally. The reason I want symbols is the conceptual weight and shared information tied up in the symbol.
I first ran into problems with this when I started working out what I wanted from my own Pagan practice. I know I’m not going to recreate a historical Pagan religious practice that will satisfy my inner pedant for accuracy, and I dislike the idea of grabbing a god and redefining it for my own use. So, I tried meditation and divination as a way to grab stuff out of my own subconscious for use. I got a bunch of god-symbol-things to work with that felt really representative of parts of myself to work with.
They’re also a bunch of problematic ideas. It turns out that my unconscious mind has a lot of toxic masculinity, racism, etc. seething just below the surface, and tapping in pulled that out, too. For my own use, I’ve come to terms with that – as long as I acknowledge the problematic aspects and don’t start assigning cosmic significance to the kyriarchical shit the inside of my skull has accumulated by growing up in this world.
It gets harder, though, when that starts being something I want to communicate with. I don’t have to tell anyone what the god-thing that represents love and dancing and joy looked like when it showed up the first couple times. But if I want to use that concept as something I put out in the world, I need a way to represent the underlying ideas without the problematic imagery my subconscious put on it.
My current problem is around a symbol for something else. I’m an old post-goth, and as such, ancient Egyptian symbolism is something I have history with. Eye of Horus eyeliner and an ankh necklace used to be a visible flag for “people like me”. A tribal signifier for a subculture of spooky kids. I’ve been wearing ankhs on and off since somewhere around the end of high school, so let’s say at least 20 years, which is a lot of time on the scale of a person. I’m wearing one now, for that matter.
Beyond the “warning: this person probably likes the Sisters of Mercy” aspect, the ankh has further personal meaning. It’s a symbol for the concept of “mystery”, for “magic” and “wisdom”. Which is a pretty idiosyncratic meaning for an ancient Egyptian symbol representing eternal life.
I can pick apart where it comes from, and how the ankh became both personally significant and where the meaning I have stuck on it accumulated. I like ankhs because they used to be what goths wore, and as a weird kid without a place to belong, that became my way of trying to connect to people I thought of as “like me”.
Where did the goths get it? From a general association of Egyptian symbolism with death and the occult that goes back to… The fucking Victorians. Who spent a lot of time and energy ripping up everything old that wasn’t nailed down from, among other places, Egypt, and carting it back home. The popularity of mummies, hieroglyphs and the book of the dead all go back to the Victorian cultural imperialism and appropriation. This especially comes into play for the goths with Aliester Crowley, who was a) big on swiping Egyptian symbolism, b) big on talking about stuff from his supposedly secret occult societies and c) liked to talk about how Dark and Wicked he was. Early goth subculture liked referencing Crowley a fair bit, and I’m comfortable pointing some blame at him.
So, I have this idea of what an ankh means for me that is rooted in a cultural context of a wealthy European country looting artifacts and ideas from “the Orient” and repurposing them for its own use. Redefining and claiming ownership of a culture for its exotic appeal. So, exactly the kind of thing that we talk about when we talk about why cultural appropriation is bad.
There is an argument that there’s a loophole for ancient Egypt (along with the old gods of Greece and Rome), that it’s the artifacts of a dead culture and a vanished religion. The people of Egypt, after all, are primarily either Coptic Christians or Muslims. The ankh isn’t a symbol of thier faith. My unease remains, though, because the whole *reason* it has meaning for me is that my culture, a few hundred years ago, looted theirs. Egypt still wants the stuff in the British Museum back.
Is there an expiration date on symbols? Can one claim that the two century pedigree of symbolism that gave me my gothic ankh of teen angst and spooky mystery is “enough” history on its own, or that Egyptian ownership of its history doesn’t come into play? It feels dodgy.
However, I can’t throw off the weight of meaning of half my life. My subconscious keeps pulling out ankhs. My graphic design skills aren’t really up to coming up with something unique but still that simple to try to attach meaning to. Basically, if I don’t use an ankh, what can I use? I also use a raven/crow for similar meanings, but a) not as visually simple, and b) there are similar problems with appropriation with Canada’s First Nations.
Maybe loot the symbols of my own culture? The ones we didn’t swipe from someone else. That pretty much leaves me trying to redefine Christianity (at which point I guess I go join the Church of Satan?) or Norse Heathenry, where I run into some reeeealy uncomfortable Nazi shit that I want nothing to do with. Furthermore, the idea that your spirituality is tied essentially to genetic descent is super problematic on its own. There are people who try to claim you can’t follow Odin unless you’re of pure Germanic descent, and now we’re right back at Nazis again.
The question boils down to wanting a symbol with no cultural baggage but with relevance and meaning. Is it possible to come up with a symbol that doesn’t have a cultural context? Corporate ad departments work really hard at this. How many random connections of lines and circles remain untrademarked in this age of melancholy elephants?
All of this is a really long whine about how I want a tattoo with an ankh in it that I think looks cool. I want the design on my body, but I don’t want to feel guilty about it.
A friend gave me a suggestion to use as a test for appropriation; no matter what, someone will think you’re an asshole for it. It’s a spectrum with white people at Coachella in feather war bonnets at one end and yoga at the other. So, how many people are you comfortable with thinking you’re an asshole? They will always be some. There is no decent place to stand, no symbol without baggage.
I guess the final question is, how much of an asshole do I think I would be for getting that tattoo, and how embarrassed will I be explaining it in 20 years?

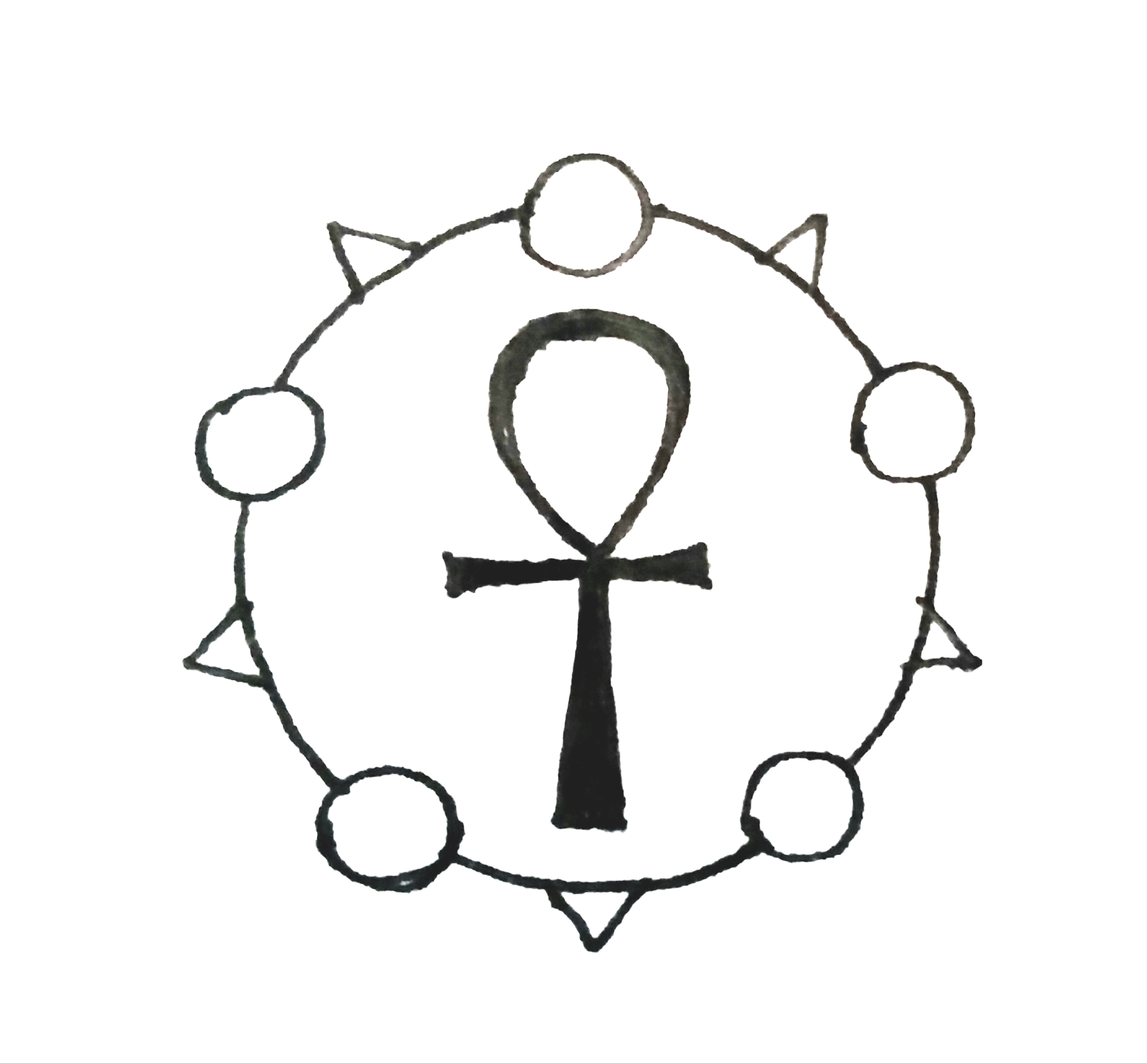
I have the exact same prob. I discovered the ankh as a child in the 70s. I’ve always worn one until about 10 years ago. I missed it, so I recently bought a new one in a necklace. I will only wear it under a shirt, because I’m afraid of offending someone.